Michelle Osmond
XML is a language for structuring data. It's actually a meta-language, a language that provides a framework (a collection of protocols and syntaxes) for creating new languages, which may be customised for particular types of data and needs. Eg, XML languages which support a specific manufacturer's product database, general chemical structures (CML), mathematical formulae (MathML), musical notation. Probably the most popular XML language is XHTML, which is a cleaned-up version of HTML (webpage language) that meets XML's stricter requirements (look at the source if you're interested - mostly it's pretty much the same as HTML). Obviously we're interested in Petri Net Markup Language (PNML).
These various languages are developed by the communities who will use them. A lot of effort goes into working out what the language will contain, and how it will be structured. It's a bit like working out an object diagram to represent data. Some relevant points are:
XML files are plain text, and certainly aren't a compact representation of data. This isn't considered to be a concern though - we're still talking about kilobyte sizes (usually), and text zips well. The big advantage of text is that they're both human- and machine-readable. You can edit them in Notepad, emacs, a text html editor or any other text editor. If you open up a valid xml file in Internet Explorer, it'll give you a nice collapsible tree that may make the file easier to visualise. The latest Mozilla also deals with XML well.
A Schema or DTD is a strict description of the syntax of the XML-language. We shouldn't need to worry too much about these, apart from for reference, or if we choose to extend the language.
XSLT is an XML transformation language, which is often used as a clever stylesheet/formatting language to manipulate XML files for display, eg searching through and only displaying certain elements, or displaying things in a particular way. This may be useful to us, as JDOM seems to support some XSLT, but I'd have to look into it further. Also, the transformation capabilities could be useful in flattening nets.
PNML has been in development for a few years. These are the basic elements:
Places - A place, which has a unique id and an initial marking.
Transitions - A transition, which has a unique id.
Arcs - An arc connecting a place and a transition. It refers to their unique id's.
Nets - Encloses Places, Transitions, and Arcs to define a Net.
Each of these elements may also contain additional information, such as a Name, a Label, and Graphics information (eg X,Y position or offset).
What's missing: the Stochastic bit. As far as I can see, there hasn't been a GSPN language defined yet. Basically, it's the transition information we need.
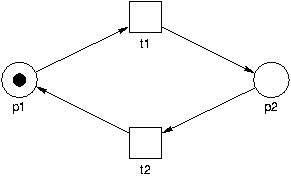
Example, taken straight from the PNML page:

<pnml xmlns="http://www.informatik.hu-berlin.de/top/pnml">
<net id="n1" type="ptNet">
<name>
<value>1-safe circle</value>
</name>
<place id="p1">
<name>
<graphics><offset page="1" x="0" y="22" /></graphics>
<value>p1</value>
</name>
<initialMarking>
<graphics><offset page="1" x="-20" y="10" /></graphics>
<value>1</value>
</initialMarking>
<graphics><position page="1" x="50" y="150" /></graphics>
</place>
<place id="p2">
<name>
<graphics><offset page="1" x="-1" y="20" /></graphics>
<value>p2</value>
</name>
<initialMarking>
<graphics><offset page="1" x="24" y="5" /></graphics>
<value>0</value>
</initialMarking>
<graphics><position page="1" x="250" y="150" /></graphics>
</place>
<transition id="t1">
<name>
<graphics><offset page="1" x="0" y="26" /></graphics>
<value>t1</value>
</name>
<graphics><position page="1" x="150" y="50" /></graphics>
</transition>
<transition id="t2">
<name>
<graphics><offset page="1" x="-1" y="22" /></graphics>
<value>t2</value>
</name>
<graphics><position page="1" x="150" y="250" /></graphics>
</transition>
<arc id="a1" source="p1" target="t1">
<inscription>
<graphics><offset page="1" x="20" y="0" /></graphics>
<value>1</value>
</inscription>
<graphics><position page="1" x="100" y="100" /></graphics>
</arc>
<arc id="a2" source="t1" target="p2">
<inscription>
<graphics><offset page="1" x="20" y="0" /></graphics>
<value>1</value>
</inscription>
<graphics><position page="1" x="200" y="100" /></graphics>
</arc>
<arc id="a3" source="p2" target="t2">
<inscription>
<graphics><offset page="1" x="20" y="0" /></graphics>
<value>1</value>
</inscription>
<graphics><position page="1" x="200" y="200" /></graphics>
</arc>
<arc id="a4" source="t2" target="p1">
<inscription>
<graphics><offset page="1" x="20" y="0" /></graphics>
<value>1</value>
</inscription>
<graphics><position page="1" x="100" y="200" /></graphics>
</arc>
</net>
</pnml>
In addition, there are two methods to introduce abstraction to the net: this does not change the net, and any file using these methods can be 'flattened' into a more basic form.
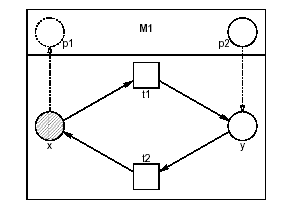 (Example from paper,
A Universal Module Concept for Petri Nets. An Implementation-Oriented Approach)
(Example from paper,
A Universal Module Concept for Petri Nets. An Implementation-Oriented Approach)
<module name="M1">
<interface>
<importPlace id="p1"/>
<exportPlace id="p2" ref="y"/>
</interface>
<referencePlace id="x" ref="p1"/>
<transition id="t1"/>
<transition id="t2"/>
<place id="y"/>
<arc source="x" target="t1"/>
<arc source="t1" target="y"/>
<arc source="y" target="t2"/>
<arc source="t2" target="x"/>
</module>

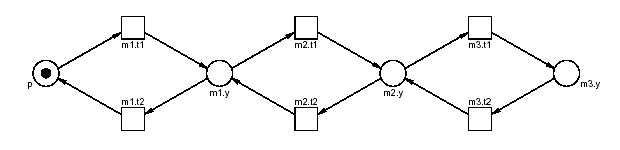
<net id="n1">
<place id="p">
<initialMarking>
<value>1</value>
</initialMarking>
</place>
<instance id="m1" ref=URI#M1>
<importPlace parameter="p1" ref="p"/>
</instance>
<instance id="m2" ref=URI#M1>
<importPlace parameter="p1" instance="m1" ref="p2"/>
</instance>
<instance id="m3" ref=URI#M1>
<importPlace parameter="p1" instance="m2" ref="p2"/>
</instance>
</net>
Arcs - one of the possible extensions is to allow for inhibitor
arcs in the simulator (but not in any of the other analysis modules
as it's too hard). The following is only relevant if we decide to do
this extension of course! It's actually possible with the implemented
PNML: however it is not in the basic PNML definition, but one of the
extensions (PNTD's). Mainly we'd be using the PNTD for a normal
Petri Net, and we'd do this by declaring our nets to be of type
"ptNet". For a net with inhibitor arcs, we'd need to use the type "ptNetArcTyped", which allows all the functionality of the ptNet type, with the
addition of one "type" attribute of the "arc" element, which may
take values "normal","read","inhibitor", or "reset". We might want
to look into what these other types of arc are, and if we want to
try implementing them too.
Actually, this isn't a real problem - more something
to consider. If we use the JDOM, we won't need to do any extra code
to allow our program to read in the special arc attributes - they'll
be stored in the DOM regardless, and we can just extract them when
we need them, the same way we extract everything else. If nothing
else, we could use this example (whether we implement it or not) as
an illustration of the extensibility of the program with respect to
supporting new types of net with add-in modules.
As mentioned before, there doesn't seem to be an extension to PNML for supporting Stochastic Petri Nets. This one is a real problem. I believe what we would be missing is the transitions - whether they are immediate/timed, and their weighting/rate of decay of the exponential distribution. We'd have to extend the PNML ourselves to store this information - deciding what elements to add. There are several possible ways of doing this:
<transition id="t1"> ... <toolspecific tool="Medusa" version="1.2"> <type>immediate</type> <weight>4.3</weight> </toolspecific> </transition>
<transition id="t1"> ... <medusa:type>immediate</medusa:type> <medusa:weight>4.3</medusa:weight> </transition>